Magnetism has been the basis for information storage for decades – first tape and disks and then hard drives. The spinning hard drive with its magnetic coating provides non-volatile and cheap data storage, though it cannot be quickly addressed like typical random access memory (RAM) in your computer (which requires power to hold its memory) and flash drive memory (which is more expensive).
When the size of a magnetic structure is on the order of a typical domain, fascinating new states may result. These states are interesting both from a fundamental physics perspective, and may have applications in magnetic random access memory – data storage that can be quickly addressed and is non-volatile. Magnetic materials may offer additional advantages like a longer shelf life or being more resistant to radiation for applications in space.
Magnetic force microscopy (MFM) offers one way of studying the states in magnetic nanostructures. Any force exerted on the tip allows us to generate an image. For MFM, we use a tip with a magnetic coating. After a first pass across the surface to determine the topography, we then raise the tip just above the surface of the sample. Magnetic fields from the sample will exert a force on the tip and change its motion, or rather, it will shift the resonance frequency of the tip proportional to the gradient of the magnetic field in the out-of-plane direction. Figure 1 shows a simulation of the MFM contrast from a dipole magnet aligned in the plane of the sample.

Figure 1: For a dipole magnet that lies in the plane, the MFM contrast would be one bright side and one dark side. Above the center of the magnet, there would be no contrast because the gradient in z is small.
With an atomic force microscope, we can not only image the state of the structure, but manipulate it as well. We do this by passing a current through a solid metal tip, generating a local, circular field that falls off in strength with increasing distance (Figure 2). This field is particularly well suited to study circularly symmetric nanostructures. Both rings and disks have a “vortex” state, in which the magnetic moments align circumferentially in the clockwise or counter-clockwise direction (Figure 3). A uniform applied field cannot select the rotation of the vortex, while the field from a current carrying wire at the center can. Simulations predict novel 360 degree domain wall states that are best understood topologically.
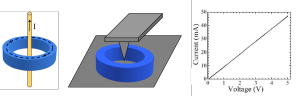
Figure 2: A current carrying wire, or the tip of an atomic force microscpe carrying current, creates a circular field that is proportional to 1/r. IV curve showing 50mA of current flowing through the tip. We have passed over 100mA through the tip.
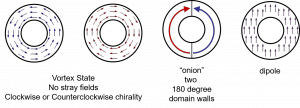
Figure 3: Common states of a thin ferromagnetic ring.
By passing current through the tip of the AFM at the center of permalloy or cobalt rings, we can switch from the onion state to the vortex state, and from CW to CCW vortex states. The vortex state shows no contrast in MFM, because the field lines are contained within the structure. By using an asymmetric ring, we have confirmed direct vortex to vortex switching. We have also shown the switching of the circulation of the vortex in a disk without changing the polarization of the vortex core.
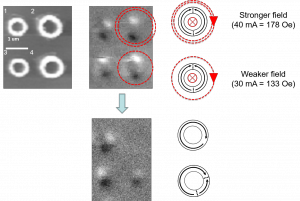
Figure 4: We apply a clockwise circular field to two of the four rings in the image. The stronger field on the top right ring annihilates the domain walls and forms the vortex state (no contrast). The weaker field moves the domain walls towards one another, but does not annihilate. See Yang et al., APL, 98, 242505(2011) for more information on this image.
In rings of certain geometries, there is a metastable state where the two 180 degree domain walls (DWs) come together but do not annihilate, as the energy required to rotate the moments is too high. When two 180 DWs meet and stabilize, they form a 360 degree DW. (360 DWs can form in non-ring geometries, as well.) By thinking about the topology of the DWs in the ring, we can better understand their formation and annihilation. Our simulations predict the formation of multiple 360 DWs for certain geometries.
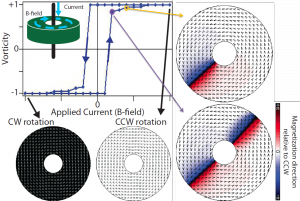
Figure 5: If we look at the hysteresis curve beginning at the bottom left, the ring is in the CW vortex state. As the applied circular field decreases in magnitude and eventually becomes a CCW field, the ring will switch to the two 360DW state with a CCW vortext (purple point on graph). Further increasing the CCW field annihilates one of the 360 DWs (yellow point) and eventually annihilates the second, forming a perfect CCW vortex.
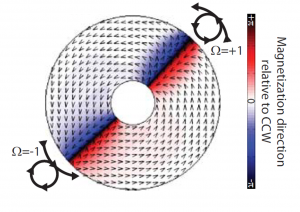
Figure 6: The two 360 DWs are not topologically identical. The top left one has a +1 winding number, which can be determined by following the rotation of the moments through the DW. As you follow the CCW vortex, the moments rotate inwards and in the CCW direction. In the bottom left DW , the moments rotate to the outside of the ring, rotating through a CW 360 degrees, giving it a winding number of =1. The +1 wall will annihilate at lower fields.